দশম শ্রেণি-দ্বিঘাত সমীকরণ কষে দেখি-1.1

এই সমস্ত অংক গুলো পশ্চিমবঙ্গ মাধ্যমিক অঙ্ক বই গণিত প্রকাশ বই থেকে নেওয়া

পাতা নাম্বার 4 থেকে 5,কষে দেখি-1.1 অধ্যায়-1

একচলবিশিষ্ট দ্বিঘাত সমীকরণ,দ্বিঘাত সমীকরণ সূত্র -বোঝার জন্য এই বাটনে ক্লিক করুন বিস্তারিত জানুন ⇉

নীচের বহুপদী সংখ্যামালার মধ্যে কোনটি/ কোনগুলি দ্বিঘাত বহুপদী সংখ্যামালা বুঝে লিখি |

---

NO.1 \(x^{2}-7x+2\)
এই অঙ্কটি দ্বিঘাত বহুপদী সংখ্যামালা |

---

NO.2 \(7x^{5}-x(x+2)\)
\(7x^{5}-x^{2}-2x\)
এটি দ্বিঘাত বহুপদী সংখ্যামালা নয় | কারণ এই সমীকরণের চলরাশির সর্বোচ্চ ঘাত (power) হলো 5

---

NO.3 \(2x(x+5)+1\)
\(2x^{2}+10x+1\)
এই অঙ্কটি দ্বিঘাত বহুপদী সংখ্যামালা |

---

NO.4 \(2x-1\)
এটি দ্বিঘাত বহুপদী সংখ্যামালা নয় | কারণ এই সমীকরণের চলরাশির সর্বোচ্চ ঘাত (power) হলো 1

NO.2 নীচের সমীকরণ গুলির কোনটি \(ax^{2}+bx+c\), যেখানে a,b,c বাস্তব সংখ্যা এবং \(a\neq 0\) আকারে লেখা যায তা লিখি |

---

NO.1 \(x-1+\frac{1}{x}=6\), (\(x\neq 0\))
\(\frac{x^{2}-x+1}{x}=6\)
\(x^{2}-x+1=6x\)
\(x^{2}-x+1-6x=0\)
\(x^{2}-7x+1=0\)

এই সমীকরণটিকে দ্বিঘাত সমীকরণ হিসেবে লেখা যায় |

---

NO.2 \(x+\frac{3}{x}=x^{2}\) , (\(x\neq 0\))
\(\frac{x^{2}+3}{x}=x^{2}\)
\(x^{2}+3=x^{3}\)
\(x^{2}-x^{3}+3=0\)

এই সমীকরণটি দ্বিঘাত সমীকরণ নয় | কারণ সর্বোচ্চ ঘাত হলো 3 |

---

NO.3 \(x^{2}-6\sqrt{x}+2\)

\(x^{2}-x^{\frac{1}{6}}+2\)

এই সমীকরণের সর্বোচ্চ ঘাত 2 | কিন্তু bx এর জায়গায় x এর পাওয়ার 1 হওয়ার কথা ছিল আর (\(b\neq 0\))| কিন্তু এখানে x এর পাওয়ার \(\frac{1}{6}\) আছে | তাই এটি দ্বিঘাত সমীকরণ নয় |

যদি b এর মান 0 হতো তাহলে এই সমীকরণটি দ্বিঘাত সমীকরণ হতো | b এর মান 0 হলে সমীকরণটি হতো \(x^{2}+2\) | কারণ 0 এর সঙ্গে \(x^{\frac{1}{6}}\) গুন করলে 0 হবে | অর্থাৎ সমীকরণটি হবে \(x^{2}-0\times x^{\frac{1}{6}}+2\)=\(x^{2}-0 +2\) =\(x^{2}+2\) | অর্থাৎ এটি একটি অমিশ্র বা শুদ্ধ দ্বিঘাত সমীকরণ | মিশ্র দ্বিঘাত সমীকরণ নয় | অমিশ্র বা শুদ্ধ দ্বিঘাত সমীকরণ ও মিশ্র দ্বিঘাত সমীকরণ কি তা জানতে এখানে ক্লিক করুন |

---

NO.4 \((x-2)^{2}=x^{2}-4x+4\)
\(x^{2}-4x+4=x^{2}-4x+4\)
\(x^{2}-4x+4-x^{2}+4x-4=0\)
0=0

NO.3 \(x^{6}-x^{3}-2=0\) সমীকরণটি চলের কোন ঘাতের সাপেক্ষে একটি দ্বিঘাত সমীকরণ তা নির্ণয় করি |

এই সমীকরণের অঙ্কতে আমরা \(x^{3}=y\) ধরিলাম | তা হলে সমীকরণের অঙ্ক টি হবে \(y^{2}-y-2=0\) | অর্থাৎ সমীকরণটি চলের \(x^{3}\) ঘাতের সাপেক্ষে একটি দ্বিঘাত সমীকরণ হবে |

NO.i \((a-2)x^{2}+3x+5=0\)সমীকরণটি a-এর কোন মানের জন্য দ্বিঘাত সমীকরণ হবে না তা নির্ণয় করি |

যদি a এর মান 2 হয় তাহলে সমীকরণটি দ্বিঘাত সমীকরণ হবে না |

কারণ \((a-2)x^{2}+3x+5=0\)
or \((2-2)x^{2}+3x+5=0\) || a এর মান 2 বসিয়ে পাই
or \(0\times x^{2}+3x+5=0\)
or \(0+3x+5=0\)

অর্থাৎ এখানে x এর সর্বোচ্চ ঘাত 1 | তাই এটি দ্বিঘাত সমীকরণ নয় |

---

NO.ii \(\frac{x}{4-x}=\frac{1}{3x}\), (\(x\neq 0, x\neq 4\))-কে \(ax^{2}+bx+c=0\) ,(\(a\neq 0\))দ্বিঘাত সমীকরণের আকারে প্রকাশ করলে x-এর সহগ কত হবে তা নির্নয় করি |

\(\frac{x}{4-x}=\frac{1}{3x}\)
OR     \(3x^{2}=4-x\)
OR     \(3x^{2}-4+x=0\)
OR     \(3x^{2}+x-4=0\)

এই অঙ্কটিকে দ্বিঘাত সমীকরণের আকারে প্রকাশ করলে x-এর সহগ 1 হবে | আর \(x^{2}\)-এর সহগ 3 হবে

---

NO.iii \(3x^{2}+7x+23=(x+4)(x+3)+2\)-কে \(ax^{2}+bx+c=0\) ,(\(a\neq 0\)) দ্বিঘাত সমীকরণ আকারে প্রকাশ করি

\(3x^{2}+7x+23=x^{2}+4x+3x+12+2\)
\(3x^{2}+7x+23=x^{2}+7x+14\)
\(3x^{2}+7x+23-x^{2}-7x-14=0\)
\(3x^{2}-x^{2}-7x+7x-14+23=0\)
\(2x^{2}+9=0\)

---

NO.iv \((x+2)^{3}=x(x^{2}-1)\)সমীকরণটিকে \(ax^{2}+bx+c=0\) ,(\(a\neq 0\)) দ্বিঘাত সমীকরণের আকারে প্রকাশ করি এবং \(x^{2}, x, x^{0}\)এর সহগ লিখি

\((x+2)^{3}=x(x^{2}-1)\)
\(x^{3}+3x^{2}2+3x2^{2}+2^{3}=x^{3}-x\)
\(x^{3}+3x^{2}2+3x2^{2}+2^{3}-x^{3}+x=0\)
\(x^{3}-x^{3}+6x^{2}+12x+8+x=0\)
\(6x^{2}+13x+8=0\)

অতএব \(x^{2}\) এর সহগ হবে 6, x এর সহগ হবে 13, \(x^{0}\) এর সহগ হবে 8

---

NO.5-i42-কে এমন দুটি অংশে বিভক্ত করি যাতে এক অংশ অপর অংশের বর্গের সমান হয় |

ধরিলাম একটি সংখ্যা হবে x | ধরিলাম অপর সংখ্যা হবে y |
তাহলে সমীকরণ হবে x+y=42
আবার অঙ্কে বলা আছে \(x=y^{2}\) || (যাতে এক অংশ অর্থাৎ x, অপর অংশের অর্থাৎ y-এর বর্গের সমান হয় | y-এর বর্গ \(y^{2}\) )
অতত্রব দ্বিঘাত সমীকরণ হবে \(y^{2}+y=42\)
\(y^{2}+y-42=0\)

---

NO.Q5-ii দুটি ক্রমিক ধনাত্মক অযুগ্ম সংখ্যার গুণফল 143

ক্রমিক সংখ্যা মানে পর পর সংখ্যা | অযুগ্ম সংখ্যা মানে 2 দ্বারা বিভাজ্য নয় এমন সংখ্যা | ধনাত্মক মানে সংখ্যার আগে (+) চিহ্ন থাকবে | ক্রমিক ধনাত্মক অযুগ্ম সংখ্যা মানে হবে 2 দ্বারা বিভাজ্য নয় এমন পর পর দুটি সংখ্যা | উদাহরণস্বরূপ বলা যেতে পারে 5,7 || 9,11 || 3,5 || 21,23 || etc

ক্রমিক ধনাত্মক অযুগ্ম সংখ্যা গুলো দেখলে বুঝতে পারব প্রথম সংখ্যা থেকে পরবর্তি সংখ্যা 2 বেশি | উপরের উদাহরণ থেকে বিষয়টি বুঝে নেওয়া যাক | 5,7 এটি একটি ক্রমিক ধনাত্মক অযুগ্ম সংখ্যা, যার প্রথম সংখ্যা 5 ও পরবর্তী সংখ্যা 7, পরবর্তী সংখ্যাটি প্রথম সংখ্যার থেকে 2 বেশি | 9,11 পরবর্তী সংখ্যাটি (11) প্রথম সংখ্যার (9) থেকে 2 বেশি অর্থাৎ 9+2=11 | 21,23---- (21+2=23) | x,x+2

ধরিলাম একটি ধনাত্মক অযুগ্ম সংখ্যা হলো x | তাহলে অপর ধনাত্মক অযুগ্ম সংখ্যা হবে x+2
শর্ত অনুযায়ী \(x\times (x+2)=143\)
\(x^{2}+2x=143\)
\(x^{2}+2x-143=0\)

---

NO.Q5-iii দুটি ক্রমিক সংখ্যার বর্গের সমষ্টি 313

ক্রমিক সংখ্যা বলতে বুঝায় পর পর সংখ্যা | উদাহরণ :-2,3 || 8,9 || 5,6 || 10,11 || 55,56 ||100,101 || x,x+1 || etc |

ধরিলাম একটি সংখ্যা হলো x | তাহলে অপর সংখ্যা হবে x+1
শর্ত অনুযায়ী \(x^{2}+(x+1)^{2}=313\)
\(x^{2}+x^{2}+2x+1^{2}=313\)
\(2x^{2}+2x+1=313\)
\(2x^{2}+2x+1-313=0\)
\(2x^{2}+2x-312=0\)
\(x^{2}+x-156=0\)

---

---

NO.i একটি আয়তাকার ক্ষেত্রের কর্ণের দৈর্ঘ্য 15 মিটার এবং তার দৈর্ঘ্য প্রস্ত অপেক্ষা 3 মিটার বেশি |

আমরা জানি আয়তাকার বস্তুর দৈর্ঘ্য ও প্রস্থ সমান হয় না | একটি বাহুর মাপ লম্বায় বড় ও অন্য বাহুর মাপ লম্বায় ছোটো হয় | অঙ্কে বলা আছে প্রস্থের থেকে দৈর্ঘ্য 3 মিটার বেশি |

ধরিলাম আয়তাকার ক্ষেত্রের প্রস্থ x মিটার | তাহলে দৈর্ঘ্য হবে x+3 মিটার |

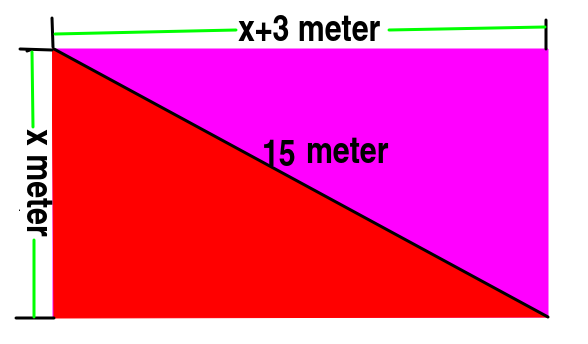
এখন লাল অংশটি একটি সমকোণী ত্রিভুজ | যার দৈর্ঘ্য x+3 মিটার, প্রস্থ x মিটার, ওত্রিভূজ 15 মিটার |

সমকোণী ত্রিভুজের সূত্র অনুযায়ী লম্ব স্কয়ার যুক্ত প্রস্থ স্কয়ার সমান ওত্রিভূজ স্কয়ার | এখানে ওত্রিভূজ হল আয়তাকার ক্ষেত্রের কর্ণ | লম্ব\(^{2}\)+ প্রস্থ\(^{2}\)=ওত্রিভূজ\(^{2}\)

তাই \((x+3)^{2}+x^{2}=15^{2}\)
\(x^{2}+6x+9+x^{2}=225\)
\(2x^{2}+6x+9-225=0\)
\(2x^{2}+6x-216=0\)
\(x^{2}+3x-108=0\)

---

NO.ii এক ব্যক্তি 80 টাকায় কয়েক কিগ্রা চিনি ক্রয় করলেন | যদি ঐ টাকায় তিনি আরও 4 কিগ্রা চিনি বেশি পেতেন, তবে তার কিগ্রা প্রতি চিনির দাম 1 টাকা কম হতো |

ধরিলা ঐ ব্যক্তি 80 টাকায় x কিগ্রা চিনি ক্রয় করলেন |
x কিগ্রা চিনির দাম 80 টাকা
1 কিগ্রা চিনির দাম \(\frac{80}{x}\) টাকা

যদি 80 টাকায় তিনি আরও 4 কিগ্রা চিনি বেশি পেতেন, অর্থাৎ x+4 কিগ্রা চিনি পেতেন তাহলে 1 কিগ্রা চিনির দাম কত হবে নির্ণয় করি |

x+4 কিগ্রা চিনির দাম 80 টাকা
1 কিগ্রা চিনির দাম \(\frac{80}{x+4}\) টাকা

শর্ত অনুযায়ী \(\frac{80}{x}-1\)= \(\frac{80}{x+4}\)

\(\frac{80}{x}-1=\frac{80}{x+4}\)

\(\frac{80}{x}-\frac{80}{x+4}=1\)

\(\frac{80x+320-80x}{x(x+4)}=1\)

\(\frac{320}{x^{2}+4x}=1\)

\(320=x^{2}+4x\)

\(320-x^{2}-4x=0\)

\(-x^{2}-4x+320=0\)

\(+x^{2}+4x-320=0\)

---

NO.iii দুটি স্টেশনের মধ্যে দুরত্ব 300 কিমি | একটি ট্রেন প্রথম স্টেশন থেকে সমবেগে দ্বিতীয় স্টেশনে গেল | ট্রেনটি গতিবেগ ঘন্টায় 5 কিমি. বেশি হলে ট্রেনটির দ্বিতীয় স্টেশনে যেতে 2 ঘন্টা কম সময় লাগত |

ধরিলাম ট্রেনটির গতিবেগ x-km/h

x-km/h গতিবেগে প্রথম স্টেশন থেকে দ্বিতীয় স্টেশন যেতে ট্রেনটির সময় লাগবে কত সময় তা প্রথমে নির্ণয় করিব |

ট্রেনটি x km দূরত্ব যায় 1 ঘন্টায়
ট্রেনটি 1 km দূরত্ব যায় \(\frac{1}{x}\) ঘন্টায়
ট্রেনটি 300 km দূরত্ব যায় \(\frac{1}{x}\times 300\) ঘন্টায়

x+5-km/h গতিবেগে প্রথম স্টেশন থেকে দ্বিতীয় স্টেশন যেতে ট্রেনটির সময় লাগবে কত সময় তা প্রথমে নির্ণয় করিব | কারণ এখানে ট্রেনটির গতিবেগ আগের গতিবেগের থেকে 5-km বেশি প্রতি ঘন্টায় | অর্থাৎ (x+5) km/h |

ট্রেনটি x+5 km দূরত্ব যায় 1 ঘন্টায়
ট্রেনটি 1 km দূরত্ব যায় \(\frac{1}{x+5}\) ঘন্টায়
ট্রেনটি 300 km দূরত্ব যায় \(\frac{1}{x+5}\times 300\) ঘন্টায়

এখন শর্ত অনুযায়ী \(\frac{1}{x}\times 300\) = \(\frac{1}{x+5}\times 300\)+2

কারণ ট্রেনটি (x+5)-km/h গতিবেগে চললে 2 ঘন্টা সময় কম লাগিব |

\(\frac{1}{x}\times 300=\frac{1}{x+5}\times 300+2\)

\(\frac{300}{x}=\frac{300}{x+5}+2\)

\(\frac{300}{x}-\frac{300}{x+5}-2=0\)

\(\frac{300\times x+300\times 5-300\times x -2\times x\times (x+5)}{x\times (x+5)}=0\)

\(\frac{300x+1500-300x -2\times (x^{2}+5x)}{x\times (x+5)}=0\)

\(\frac{300x+1500-300x -2(x^{2}+10x)}{x\times (x+5)}=0\)

\(1500 -2x^{2}-10x=0\times x\times (x+5)\)

\(1500 -2x^{2}-10x=0\)

\(-2x^{2}-10x+1500=0\)

\(-x^{2}-5x+750=0\)

\(x^{2}+5x-750=0\)

---

NO.iv একজন ঘড়ি বিক্রেতা একটি ঘড়ি ক্রয় করে 336 টাকায় বিক্রি করলেন। তিনি যত টাকায় ঘড়িটি ক্রয় করেছিলেন শতকরা তত টাকা তাঁর লাভ হলো।

ধরিলাম x টাকায় একটি ঘড়ি ক্রয় করেন
তাহলে লাভ করেন 336-x টাকা

এখন আমাকে নির্ণয় করতে হবে 100 টাকায় ঘড়িটি ক্রয় করলে কত টাকা লাভ করবেন |

x টাকা ক্রয় মূল্য হলে লাভ হয় 336-x টাকা
1 টাকা ক্রয় মূল্য হলে লাভ হয় \(\frac{336-x}{x} \)টাকা
100 টাকা ক্রয় মূল্য হলে লাভ হয় \(\frac{336-x}{x}\times 100 \) টাকা

এখন প্রশ্ন হলো 100 টাকায় ঘড়িটি ক্রয় করিল এবং ঘড়িটি বিক্রি করে যে পরিমাণ লাভ করেন, সেই লাভের পরিমাণ- ই হল ঘড়িটির আসল দাম | অর্থাৎ \(\frac{336-x}{x}\times 100 \) টাকা = x টাকা

\(\frac{336-x}{x}\times 100 \) = x

\(\frac{33600-100x}{x}\) = x

\(33600-100x=x^{2}\)

\(33600-100x-x^{2}=0\)

\(-x^{2}-100x+33600=0\)

\(+x^{2}+100x-33600=0\)

---

NO.v স্রোতের বেগ ঘণ্টায় 2 কিমি. হলে, রতনমাঝির স্রোতের অনুকূলে 21 কিমি. গিয়ে ওই দুরত্ব ফিরে আসতে 10 ঘণ্টা সময় লাগে।

এই দ্বিঘাত সমীকরণের অঙ্কটি-তে একটি নৌকা প্রথমে এক স্থান থেকে যাত্রা সুরু করে অপর একটি স্থানে পৌছলেন (অনুকূলে যাওয়া)| তারপর অপরস্থান থেকে পুনরায় আগের স্থানে ফিরে আসে (প্রতিকূলে আসা)| এই অনুকূলে যাওয়া ও প্রতিকূলে ফিরে আসার মোট সময় লাগে 10 ঘন্টা | প্রতিকূলে মানে নদীর স্রোতের বিপরীত দিকে নৌকা চালানো | অনুকূলে মানে নদীর স্রোত যেই দিকে চলে সেই দিকে নৌকা চালানো |

ধরিলাম স্থির জলে নৌকার বেগ x-km/h
অনুকূলে নৌকার বেগ (x+2)-km/h
প্রতিকূলে নৌকার বেগ (x-2)-km/h

অর্থাৎ নৌকাটি 21 km স্রোতের অনুকূলে যাবে, আর নৌকাটি 21 km স্রোতের প্রতিকূলে ফিরে আসবে |

তাহলে স্রোতের অনুকূলে 21 km যেতে কত সময় লাগবে নির্ণয় করি
স্রোতের অনুকূলে (x+2) km নৌকাটি যায় 1 ঘন্টায়
স্রোতের অনুকূলে 1 km নৌকাটি যায় \(\frac{1}{x+2}\) ঘন্টায়
স্রোতের অনুকূলে 21 km নৌকাটি যায় \(\frac{1}{x+2}\times 21\) ঘন্টায়

তাহলে স্রোতের প্রতিকূলে 21 km যেতে কত সময় লাগবে নির্ণয় করি
স্রোতের প্রতিকূলে (x-2) km নৌকাটি যায় 1 ঘন্টায়
স্রোতের প্রতিকূলে 1 km নৌকাটি যায় \(\frac{1}{x-2}\) ঘন্টায়
স্রোতের প্রতিকূলে 21 km নৌকাটি যায় \(\frac{1}{x-2}\times 21\) ঘন্টায়

এখন শর্ত অনুযায়ী \(\frac{1}{x+2}\times 21\) ঘন্টা + \(\frac{1}{x-2}\times 21\) ঘন্টা =10 ঘন্টা

\(\frac{1}{x+2}\times 21+\frac{1}{x-2}\times 21=10\)

\(\frac{21}{x+2}+\frac{21}{x-2}=10\)

\(\frac{21\times(x-2)+21\times(x+2)}{(x+2)(x-2)}=10\)

\(\frac{21x-42+21x+42}{(x+2)(x-2)}=10\)

\(\frac{21x+21x}{(x+2)(x-2)}=10\)

\(\frac{42x}{(x+2)(x-2)}=10\)

\(\frac{42x}{x^{2}-2^{2}}=10\)

\(\frac{42x}{x^{2}-4}=10\)

\(42x=10\times x^{2}-10\times 4\)

\(42x=10x^{2}-40\)

\(42x-10x^{2}+40=0\)

\(-10x^{2}+42x+40=0\)

\(10x^{2}-42x-40=0\)

\(5x^{2}-21x-20=0\)

---

NO.vi আমাদের বাড়ির বাগান পরিষ্কার করতে মহিম অপেক্ষা মজিদের 3 ঘন্টা বেশি সময় লাগে। তারা উভয়ে একসঙ্গে কাজটি 2 ঘন্টায় শেষ করতে পারে।

এখানে দুজন ব্যক্তি মহিম ও মজিদ আলাদা আলাদা ভাবে একটি কাজ কত সময়ে করিতে পারবে তা নির্নয় করি |

ধরিলাম মহিম একটি কাজ করিতে সময় নেয় x ঘন্টা
অতএব মজিদ একটি কাজ করিতে সময় নেয় x+3 ঘন্টা

এখন দুজন মিলে কাজটি একসঙ্গে করলে কত সময়ে সম্পূর্ণ করতে পারবে তা নির্নয় করি |

মহিম x ঘন্টায় কাজটির করিবে 1 অংশ
মহিম 1 ঘন্টায় কাজটির করিবে \(\frac{1}{x}\) অংশ

মজিদ x+3 ঘন্টায় কাজটির করিবে 1 অংশ
মজিদ 1 ঘন্টায় কাজটির করিবে \(\frac{1}{x+3}\) অংশ

এখন দুজনে মিলে 1 ঘন্টা কাজটির \(\frac{1}{x}\) + \(\frac{1}{x}\) অংশ করিতে পারে
এখন দুজনে মিলে \(\frac{1}{x} + \frac{1}{x+3}\) অংশ করে 1 ঘন্টায়
দুজনে মিলে 1 অংশ করে \(\frac{1}{\frac{1}{x} + \frac{1}{x+3}}\) ঘন্টায়
\(\frac{1}{\frac{x+3+x}{x^{2}+3x}}\)

\(\frac{x^{2}+3x}{x+3+x}\)

\(\frac{x^{2}+3x}{2x+3}\)

এখন শর্ত অনুযায়ী \(\frac{x^{2}+3x}{2x+3}=2\)

\(\frac{x^{2}+3x}{2x+3}=2\)

\(x^{2}+3x=4x+6\)

\(x^{2}+3x-4x-6=0\)

\(x^{2}-x-6=0\)

---

NO.vii দুই অঙ্কবিশিষ্ট একটি সংখ্যার একক স্থানীয় অঙ্কটি দশক স্থানীয় অঙ্ক অপেক্ষা 6 বেশি এবং অঙ্কদ্বয়ের গুণফল সংখ্যাটির চেয়ে 12 কম।

ধরিলাম দশক স্থানীয় অঙ্কটি হল x | তা হলে একক স্থানীয় অঙ্কটি হবে x+6 | আর সংখ্যাটি হবে (10x)+(x+6)=10x+x+6=11x+6 | আর অঙ্ক দুটির গুণফল হবে \(x\times (x+6)\) = \(x^{2}+6x\)

দশক স্থানীয় অঙ্ক x
একক স্থানীয় অঙ্ক x+6
সংখ্যাটি 11x+6
অঙ্ক দুটির গুণফল \(x^{2}+6x\)

এখন সমীকরণটি হবে \(x^{2}+6x\) = (11x+6)-12
\(x^{2}+6x\) = 11x+6-12
\(x^{2}+6x = 11x-6\)
\(x^{2}+6x -11x+6=0\)
\(x^{2}-5x+6=0\)

---

NO.viii 45 মিটার দীর্ঘ ও 40 মিটার প্রশস্ত একটি আয়তক্ষেত্রাকার খেলার মাঠের বাইরের চারিপাশে সমান চওড়া একটি রাস্তা আছে এবং ওই রাস্তার ক্ষেত্রফল 450 বর্গ মিটার।

ধরিলাম আয়তক্ষেত্রাকার মাঠের চারপাশে যে রাস্তা রয়েছে সেই রাস্তাটি x মিটার চওড়া | মাঠের বাইরে রাস্তা তৈরি করার জন্য মাঠের বাইরে একটি আয়তক্ষেত্র তৌরি হলো | এখন প্রথমে মাঠের ক্ষেত্রফল নির্ণয় করিব | তার পর মাঠ সমেত রাস্তার ক্ষেত্রফল নির্ণয় করিব | তার পর মাঠ সমেত রাস্তার ক্ষেত্রফল থেকে মাঠের ক্ষেত্রফল বিয়োগ করিলে মাঠের বাইরে রাস্তার ক্ষেত্রফল পাওয়া যাবে |

মাঠের ক্ষেত্রফল \(45\times 40\) বর্গ মিটার, 1800 বর্গ মিটার |

মাঠ সমেত রাস্তার ক্ষেত্রফল নির্ণয় করতে হলে দৈর্ঘ্য ও প্রস্থ কত হবে তা দেখে নেওয়া যাক | দৈর্ঘ্য হবে x+45+x=2x+45 মিটার, আর প্রস্থ হবে x+40+x=2x+40 মিটার | আর ক্ষেত্রফল হবে \((2x+45)\times (2x+40)\) বর্গ মিটার |

তাহলে রাস্তার ক্ষেত্রফল হবে \((2x+45)\times (2x+40)\) বর্গ মিটার (-)বিযুক্ত (\(45\times 40\)) বর্গ মিটার = \(4x^{2}+45\times 2x+2x\times 40+ 45\times 40-45\times 40\)=\(4x^{2}+90x+80x+ 1800-1800\)=\(4x^{2}+170x\)

এখন শর্ত অনুযায়ী \(4x^{2}+170x=450\) | কারণ রাস্তার ক্ষেত্রফল বইতে 450 উল্লেখ করা আছে |
সমাধান \(4x^{2}+170x=450\)
\(4x^{2}+170x-450=0\)
\(2x^{2}+85x-225=0\)

---

অন্য নিয়মে এই 8 নম্বর অঙ্কের দ্বিঘাত সমীকরণ গঠন করে দেখি

ধরিলাম আয়তক্ষেত্রাকার মাঠের চারপাশে যে রাস্তা রয়েছে সেই রাস্তাটি x মিটার চওড়া | তাহলে রাস্তার ক্ষেত্রফল এখন নির্ণয় করব | ছবিতে        বেগুনি কালার ও        লাল কালার মিলে যে অংশ রয়েছে তার ক্ষেত্রফল নির্ণয় করব | এটি হলো আয়তক্ষেত্রাকার মাঠের চারপাশের রাস্তা | একটি ছবির সাহায্যে বিষয়টি বুঝে নেওয়া যাক |

প্রথমে লাল অংশ বাদ দিয়ে রাস্তার ক্ষেত্রফল নির্ণয় করা হয়েছে | শুধু বেগুনি অংশ রাস্তার ক্ষেত্রফল নির্ণয় করা হয়েছে | আয়তক্ষেত্রাকার মাঠের এক দিকের দৈর্ঘ্য বরাবর রাস্তার ক্ষেত্রফল হবে \(45\times x\) | আয়তক্ষেত্রাকার মাঠের দুই দিকের দৈর্ঘ্য বরাবর রাস্তার মোট ক্ষেত্রফল হবে \(45\times x\) + \(45\times x\) = \(90\times x\) | কারণ আয়তক্ষেত্রাকার মাঠের দৈর্ঘ্য রাস্তার দৈর্ঘ্য হিসেবে মনে করা হয়েছে | আর রাস্তার প্রস্থ হলো x মিটার, কারণ রাস্তাটি x মিটার চওড়া | |||| একই রকমভাবে আয়তক্ষেত্রাকার মাঠের এক দিকের প্রশস্ত বরাবর রাস্তার ক্ষেত্রফল হবে \(40\times x\) | আয়তক্ষেত্রাকার মাঠের দুই দিকের প্রশস্ত বরাবর রাস্তার মোট ক্ষেত্রফল হবে \(40\times x\) + \(40\times x\) = \(80\times x\) | এখানে আয়তক্ষেত্রাকার মাঠের প্রস্থ রাস্তার দৈর্ঘ্য হিসেবে নেওয়া হয়েছে | রাস্তাটির প্রস্থ x মিটার চওড়া |||| এখন লাল অংশ বাদ দিলে রাস্তাটি সম্পন্ন হবে না | তাই লাল অংশের ক্ষেত্রফল নির্ণয় করতে হবে | লাল অংশটি একটি বর্গক্ষেত্র, যার বাহুর দৈর্ঘ্য x মিটার, ও ক্ষেত্রফল \(x^{2}\) বর্গ মিটার | তবে চারটি লাল অংশের ক্ষেত্রফল হবে \(x^{2}+x^{2}+x^{2}+x^{2}\) বর্গ মিটার = \(4x^{2}\) বর্গ মিটার |||| এখন মাঠের দুই দিকের দৈর্ঘ্য বরাবর রাস্তা ও দুই দিকের প্রশস্ত বরাবর রাস্তা ও মাঠের চারদিকের চারটি কোনের বাড়তি রাস্তা যোগ করলে মোট রাস্তর ক্ষেত্রফল পাবো | \(90\times x\)+\(80\times x\)+\(4x^{2}\) বর্গ মিটার = \(90\times x+80\times x+4x^{2}\) = \(4x^{2}+170x\) বর্গ মিটার | নিচের ছবিটির সাথে মিলিয়ে বিষয়টি ভালো ভাবে বুঝে নিবো |

শর্ত অনুযায়ী \(4x^{2}+170x = 450\)
সমাধান \(4x^{2}+170x=450\)
\(4x^{2}+170x-450=0\)
\(2x^{2}+85x-225=0\)