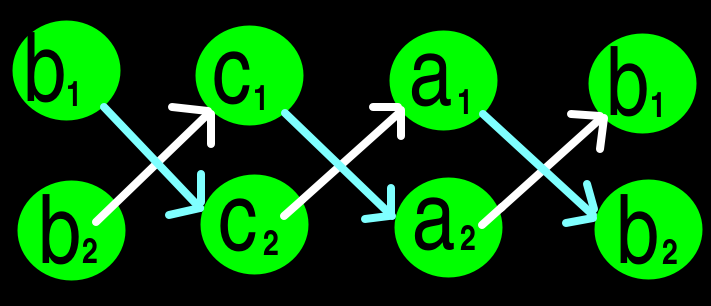
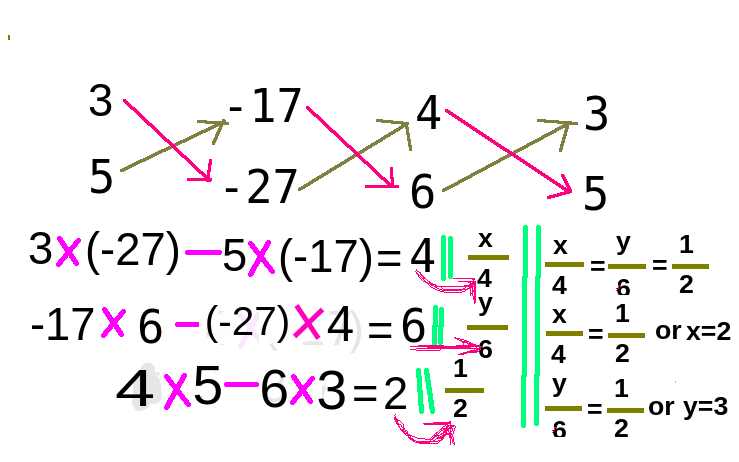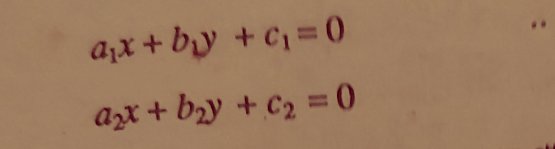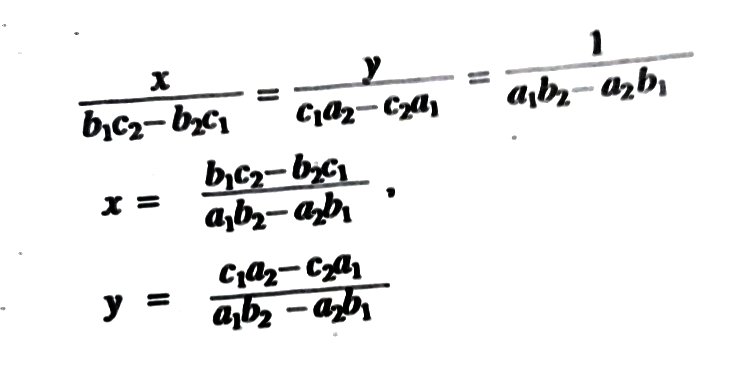সমীকরণ এবং দ্বিঘাত সমীকরণ গঠন করার পদ্ধতি ও তার সমাধান

এই পৃষ্ঠায় আমরা সমীকরণ এবং দ্বিঘাত সমীকরণ গঠন ও তার সমাধান নিয়ে আলোচনা করিব | এই বাটন গুলো স্পর্শ করে সরাসরি সেই স্থানে পৌঁছে যাব |

উদাহরণ:- বাপনের 4 টি কলম আছে | উত্তমের 7 টি কলম আছে | কি করলে বাপন ও উত্তম এর কলম সমান হবে | বাপন এর কলম এর সঙ্গে আরো 3টি কলম যোগ করলে উত্তমের কলমের সমান হবে | [অর্থাৎ:- বাপন এর কলম+3টি কলম=উত্তমের কলম] |আর বামপক্ষ হল:- বাপন এর কলম+3টি কলম ও ডানপক্ষ হল:- উত্তমের কলম | বামপক্ষে 3টি কলম যোগ করিলে ডানপক্ষ এর সমান হবে | অথবা উত্তম এর কলম থেকে 3 টি কলম সরিয়ে নিলে অর্থাৎ বিয়োগ করিলে বাপনের কলমের সমান হবে | [অর্থাৎ:- বাপন এর কলম=উত্তমের কলম-3টি কলম] |এখানে ডানপক্ষে 3 টি কলম বিয়োগ করিলে বামপক্ষ এর সমান হবে |এখানে উত্তর হলো 3, | এই উত্তর, পাটিগণিতের যোগ বিয়োগ এর নামতা এর সাহায্যে নিয়ে খুব সহজেই উত্তর 3 বের করে নিলাম | কিন্তু বামপক্ষ ও ডানপক্ষের সংখ্যা গুলি যদি বড় হয়, তখন মুখে মুখে নামতার সাহায্য নিয়ে উত্তর নির্ণয় করা কঠিন হবে |

এই কঠিন সমস্যা সমাধান করার জন্য প্রয়োজন হয় বীজগণিত এর অঙ্ক | এই অঙ্কে আমি উত্তর পেলাম 3 | অঙ্কটি করার আগে আমি উত্তর টি জানিতাম না | তাই উত্তরটি হলো একটি অজানা সংখ্যা বা রাশি | সমাধান করার পর এই অজানা সংখ্যা বা রাশির মান জানতে পারিলাম | বীজ গতিতে প্রথমে এই অজ্ঞাত রাশির মান ধরে নিলাম | সাধারণত ইংরেজি বর্ণমালা এর a থেকে z এর মধ্যে কোনো একটি বর্ণকে অজ্ঞাত রাশি হিসেবে ধরে নেওয়া হয় | তারপর বীজগণিতের নিয়ম অনুযায়ী সমাধান করে ধরে নেওয়া রাশির মান নির্ণয় করা হয় অর্থাৎ নির্ণয় করা রাশির মান এখানে 3 পেলাম |

বীজগণিতের সাহায্যে অংকটি কিভাবে করব তা দেখে নেওয়া যাক

step-1;ধরিলাম বাপনের কলমের সঙ্গে x টি কলম যোগ করিলে উত্তমের কাছে থাকা কলমের পরিমাণের সমান হবে |

শর্ত অনুযায়ী 4+x=7
x=7-4
x=3

বামপক্ষ	ডানপক্ষ
4+x	7
x	7-4
x	3

step-2;ধরিলাম উত্তমের কলমের সঙ্গে x টি কলম বিয়োগ করিলে বাপনের কাছে থাকা কলমের পরিমাণের সমান হবে |

শর্ত অনুযায়ী 4=7-x
4-7=-x
-3=-x
x=3

বামপক্ষ	ডানপক্ষ
4	7-x
4-7	-x
-3	-x
x	3

সমীকরণের অংকটি সহজ ভাবে বোঝার জন্য একটি সাধারণ দাঁড়িপাল্লা নিবো | একটি সাধারণ দাঁড়িপাল্লা এর বাম দিকের পাল্লায় 4 টি কলম ও ডান দিকের পাল্লায় 7 টি কলম রাখিলাম | কলম গুলি রাখার পর দেখতে পাবো ডান দিকের পাল্লাটি ভারি হবে, অর্থাৎ ডান দিকের পাল্লাটি মাটির দিকে বেশি ঝুকে থাকবে | কি করলে বাম দিকের পাল্লা ও ডান দিকের পাল্লা দুটি সামান হবে, অর্থাৎ দাঁড়িপাল্লাটি অনুভূমিক অবস্থায় আসবে চিন্তা করি |

আমরা বাম দিকের পাল্লা টির মধ্যে আরো 3 টি কলম রাখিলাম, ফলে বাম দিকের পাল্লা টির মধ্যে 4+3=7 টি কলম হলো | এই কারনে বাম দিকের পাল্লা এর মধ্যে 7 টি কলম ও ডান দিকের পাল্লা এর মধ্যে 7 টি কলম হয়েছে | এতে দাঁড়িপাল্লাটি অনুভূমিক অবস্থায় এসেছে |
অন্য রকম ভাবে করিলে ডান দিকের পাল্লা টির মধ্যে থেকে 3 টি কলম তুলে নিলাম, ফলে ডান দিকের পাল্লা টির মধ্যে 7-3=4 টি কলম হলো | এই কারনে বাম দিকের পাল্লা এর মধ্যে 4 টি কলম ও ডান দিকের পাল্লা এর মধ্যে 4 টি কলম হয়েছে | এতে দাঁড়িপাল্লাটি অনুভূমিক অবস্থায় এসেছে |

( এখানে কলম গুলির ওজন সমান )
সমীকরণের অংক গুলো করতে গেলে দাঁড়িপাল্লার মতো ডান দিক ও বাম দিক সব সময় সমান রাখতে হয় |

এখানে আমরা অঙ্কটি তে বীজগাণিতিক প্রতীক ব্যবহার করে সমস্যাটিকে গাণিতিক ভাষায় প্রকাশ করলাম | গণিতের ভাষায় এই পদ্ধতিকে বলা হয় সমীকরণ গঠন করা | সমীকরণ গঠন করার পর সমস্যাটি সমাধান করে অজানা রাশির মান নির্নয় করা হয় | অজানা রাশি বলতে বোঝানো হয়েছে বীজগণিতের চলরাশির |

সমীকরণের বীজ

সমীকরণ সমাধান করার পর অজানা রাশির অর্থাৎ x এর একটি নির্দিষ্ট বাস্তব মান পেলাম | এই বাস্তব মান সমীকরণে এর দুই পক্ষকে সমান করে | অর্থাৎ সমাধান করার পর পাওয়া বাস্তব মান টি সমীকরণে বসালে সমীকরন এর বামপক্ষ = ডানপক্ষ হবে | 4=7-x সমীকরণ টি সমাধান করলে x এর মান বের হবে 3 | সমীকরণে x এর পরিবর্তে 3 বসালে সমীকরণের দুই পক্ষ সমান হবে | 4=7-3 or 4=4

সংজ্ঞা:- অজানা সংখ্যার যে সুনির্দিষ্ট মান সমীকরণের উভয় পক্ষের মান সমান করে বা সিদ্ধ করে, তাকে সমীকরণের বীজ বলে |

আর এই অজানা রাশির মান নির্ণয় করার প্রক্রিয়াকে বলা হয় সমীকরণ সমাধান করা |

সমীকরণ সমাধানের নিয়ম | সমীকরণ সমাধান করার কতগুলি নিয়ম নিয়ে আলোচনা করা যায় |

সমীকরণের পক্ষান্তর প্রক্রিয়া কি ?

সমীকরণের পাটি গাণিতিক বা বীজগাণিতিক সংখ্যা বা সংখ্যামালা = চিহ্নের একপাশ থেকে অপর পাশে নিয়ে যাওয়ার এই প্রক্রিয়াকে গানিতিক ভাষায় বলা হয় পক্ষান্তর প্রক্রিয়া |

অর্থাৎ সমীকরণের সমাধান করার সময় ডানপক্ষ থেকে বামপক্ষে আবার বামপক্ষ থেকে ডানপক্ষে পাটি গাণিতিক বা বীজগাণিতিক সংখ্যা বা সংখ্যামালা এর স্থানান্তর করার পদ্ধতি কে বলা হয় পক্ষান্তর প্রক্রিয়া |

একটি সমীকরণের ডানপক্ষ থেকে বামপক্ষে কিম্বা বামপক্ষ থেকে ডানপকক্ষে কোনো সংখ্যা স্থানান্তর হলে কি হবে দেখে নেওয়া যাক | অর্থাৎ = চিহ্নের ডানদিক থেকে বামদিক অথবা বামদিক থেকে ডান দিক কোন সংখ্যা স্থানান্তর হলে কি হবে দেখে নেওয়া যাক

সমীকরণ সমাধানের সময় ডানপক্ষ এর চিহ্ন গুলি স্থান পরিবর্তন করে বাম পক্ষে এলে কি হবে দেখে নেওয়া যাক |

সমীকরণের ডান দিকের অংশে অর্থাৎ ডান পক্ষে কোনো সংখ্যার আগে যুক্ত চিহ্ন থাকলে তা বাম দিকে এলে সেই সংখ্যার আগে বিয়োগ চিহ্ন হবে |
বিয়োগ চিহ্ন থাকলে বাম দিকে এলে তা যুক্ত চিহ্ন হবে |
গুন থাকলে বাম দিকে এলে তা ভাগ হবে |
ভাগ থাকলে বাম দিকে এলে তা গুণ হবে |

ডান পক্ষে	বাম পক্ষে
+	-
-	+
\(\times\)	\(\div\)
\(\div\)	\(\times\)
পক্ষান্তর প্রক্রিয়া এর উদাহরণ
x +2=5+7	x=5+7-2
x+6+9=5	x+6=5-9
x\(\times\)3=6\(\times\)2	x=6\(\times\)2 \(\div\)3
x\(\div\)5=6	x=6\(\times\)5

সমীকরণ সমাধানের সময় বামপক্ষ এর চিহ্ন গুলি স্থান পরিবর্তন করে ডানপক্ষে এলে কি হবে দেখে নেওয়া যাক |

সমীকরণের বাম দিকের অংশে অর্থাৎ বামপক্ষে কোনো সংখ্যার আগে যুক্ত চিহ্ন থাকলে তা ডান দিকে এলে সেই সংখ্যার আগে বিয়োগ চিহ্ন হবে |
বিয়োগ চিহ্ন থাকলে ডান দিকে এলে তা যুক্ত চিহ্ন হবে |
গুন থাকলে ডান দিকে এলে তা ভাগ হবে |
ভাগ থাকলে ডান দিকে এলে তা গুণ হবে |

বাম পক্ষে	ডান পক্ষে
+	-
-	+
\(\times\)	\(\div\)
\(\div\)	\(\times\)
উদাহরণ গুলি উপরের ছকের মতো হবে

কতগুলি পদ্ধতি এর সাহায্যে সমীকরণ এর সমতা অপরিবর্তিত রাখা হয় | পদ্ধতি গুলি হল নিম্নরূপ |

সমীকরণের উভয় পক্ষের সঙ্গে সমান সংখ্যক সংখ্যা যোগ করা যায় | অর্থাৎ বামপক্ষে 5 যোগ করিলে ডানপক্ষের সঙ্গে 5 যোগ করিতে হয় | তবে সমীকরণ টি সমান থাকবে |
একি রকম ভাবে সমীকরণের উভয় পক্ষের সঙ্গে সমান সংখ্যক সংখ্যা বিয়োগ করা যায় | অর্থাৎ বামপক্ষে 9 বিয়োগ করিলে ডানপক্ষের সঙ্গে 9 বিয়োগ করিতে হয় | এতে সমীকরণ এর মনের কোনো পরিবর্তন হবে না |
উভয় পক্ষকে একই সংখ্যা দিয়ে গুণ করা যায় |
উভয় পক্ষকে একই সংখ্যা দিয়ে ভাগ করা যায় |

NO:-1

সমীকরণ	যোগ করার পর সমীকরণ
x+3=7	x+3+ 5=7+5
দুই পক্ষে 5 যোগ করার পর মানের কোনো পরিবর্তন হবে না

NO:-2

সমীকরণ	বিয়োগ করার পর সমীকরণ
x+3=7	x+3- 9=7-9
দুই পক্ষে 9 বিয়োগ করার পর মানের কোনো পরিবর্তন হবে না

NO:-3

সমীকরণ	গুণ করার পর সমীকরণ
x+3=7	(x+3)\(\times\)2=7\(\times\)2
দুই পক্ষে 2 গুণ করার পর মানের কোনো পরিবর্তন হবে না

NO:-4

সমীকরণ	ভাগ করার পর সমীকরণ
x+3=7	(x+3)\(\div\) 4=7\(\div\) 4
দুই পক্ষে 4 ভাগ করার পর মানের কোনো পরিবর্তন হবে না

এক ঘাত বিশিষ্ট সরল সমীকরণ

উপরে আমরা পড়লাম সমীকরণ কি ও কিভাবে তা গঠন ও সমাধান করা হয় | এখানে আলোচিত সমীকরণের একটি মাত্র বীজগাণিতিক চলরাশি এর আলোচনা করা হয়েছে | বীজগাণিতিক চলরাশি হলো একটি অজ্ঞাত সংখ্যা | আমাদের এই চলরাশি অর্থাৎ অজ্ঞাত সংখ্যা এর মান নির্ণয় করতে হয় |

এক ঘাত বিশিষ্ট সরল সমীকরণ কাকে বলে

ANS:- যে সরল সমীকরণ এ সর্বচ্চ এক ঘাত বিশিষ্ট অজ্ঞাত সংখ্যা আছে সেই সমীকরণকে বলা হয় এক ঘাত বিশিষ্ট সরল সমীকরণ | এই সরল সমীকরণ এর অঙ্কগুলি তে অজানা রাশির পাওয়ার 1 হয় অর্থাৎ ঘাত 1 হয় বলে এক ঘাত বিশিষ্ট সমিকরন বলা হয় | উদাহরণ এর মাধ্যমে বুঝে নেওয়া যাক | এখানে আমরা চলরাশির মান x ধরে অঙ্ক গুলি করিলাম |

সরল সমীকরণ
\(x^{1}+5=3\)
\(7-x^{1}=5\)
\(10-x^{1}-2=0\)
ETC

x পাওয়ার 1 হলে অর্থাৎ \(x^{1}\) হলে, x এর মাথার উপর 1 লিখা হয় না | \(x^{1}\) পরিবর্তে x লিখা হয় |

একটি উদাহরণের মাধ্যমে সরল সমীকরণ কিভাবে গঠন করবো তা দেখে নেওয়া যাক

একটি অঙ্ক পরীক্ষায় দুই বন্ধুর পাওয়া মোট নম্বর হল 117 , প্রথম বন্ধু বাপন যত নম্বর পেয়েছে তার থেকে 7 নম্বর বেশি পেয়েছে দ্বিতীয় বন্ধু উত্তম | তা হলে কোন বন্ধু কত নাম্বার পেয়েছে নির্ণয় করি |

ধরিলাম বাপন অঙ্ক পরীক্ষায় নম্বর পেয়েছে x
তা হলে উত্তম অঙ্ক পরীক্ষায় নম্বর পাবে x+7

শর্ত অনুযায়ী
বাপন + উত্তম	= 117
(x)+(x+7)	=117
x+x+7	=117
2x+7	=117
এটি হলো এক চল বিশিষ্ট একঘাত সমীকরণ গঠন করার পদ্ধতি

সহ সমীকরণ

এক-চল বিশিষ্ট সমীকরণ গঠন করার পদ্ধতি আমরা শিখেছি | অনেক সময় সমীকরণ গঠন করতে আমাদের প্রয়োজন হয় দুটি চলরাশির | এই দুটি চলরাশি দিয়ে দুটি সমীকরণ গঠন করা হয় | উপরের উদাহরণ টি আরেকবার বুঝে নেওয়া যাক |

এই অঙ্কটি আমি আগে একচল রাশির এর সাহায্যে সমাধান করেছি | এখন দুটি চল রাশির এর সাহায্যে সমাধান করিব |

ধরিলাম বাপন অঙ্ক পরীক্ষায় নম্বর পেয়েছে x আর উত্তম নম্বর পেয়েছে y | এখানে আমি দুটি চলরাশি x ও y ধরিলাম |
তাহলে সমীকরণ দুটি হবে
x+y=117--------1.Noসমীকরণ | (কারণ দুজনের মোট নাম্বার)
y-x=7--------2.Noসমীকরণ |(দুই বন্ধুর নম্বরের পার্থক্য 7)

এই সমীকরণ দুটিকে একসঙ্গে বলা হয় সহ সমীকরণ | এই সমীকরণ দুটির মধ্যে একটি সমস্যার সমাধান রয়েছে | একটি সমীকরণ অন্য একটি সমীকরণ এর উপর নির্ভরশিল | একটি সমীকরণ সমাধান করে আমরা সমস্যাটির সম্পূর্ণ উত্তর অর্থাৎ নির্দিষ্ট উত্তর পাবো না | সমীকরণ দুটিকে একসঙ্গে সূত্র অনুযায়ী সমাধান করতে হবে | সহসমীকরণ এর সমাধান সূত্র গুলি হল নিম্নরূপ |

সহ সমীকরণ সমাধান করার জন্য প্রধানত চারটি সূত্র এর সাহায্য নিতে হয় | চারটি পদ্ধতি মধ্যে যে কোনো একটি পদ্ধতি এর সাহায্য নিয়ে সমাধান করা হয় | পদ্ধতি গুলি হল নিম্নরূপ |

তুলনামূলক পদ্ধতি(Method of Comparison)
পরিবর্ত পদ্ধতি(Method of Substitution)
অপনয়ন পদ্ধতি(Method of Elimination)
বজ্রগুণন পদ্ধতি(Method of Cross-multiplication)

তুলনামূলক পদ্ধতি(Method of Comparison)

এই নিয়মে 1.NO ও 2.NO সমীকরণ থেকে আলাদা আলাদা চলরাশি x এর মান নির্ণয় করব | ডানপক্ষে x রেখে বামপক্ষে x এর মান নিয়ে নতুন সমীকরণ নির্ণর করা হল | 1.NO সমীকরণ থেকে পাওয়া সমীকরণ এর নাম দিলাম 3.NO সমীকরণ | ও 2.NO সমীকরণ থেকে পাওয়া সমীকরণ এর নাম দিলাম 4.NO সমীকরণ | এই 3.NO ও 4.NO সমীকরণ দুটির ডানপক্ষে থাকবে x | একটি উদাহরণের মাধ্যমে বিষয়টি বুঝে নেওয়া যাক |

x+y=117--------1.Noসমীকরণ
y-x=7--------2.Noসমীকরণ

x+y=117--------1.Noসমীকরণ
x=117-y
x=117-y --------3.Noসমীকরণ তৈরি করা হল

y-x=7--------2.Noসমীকরণ
-x=7-y
+x=-7+y (সমীকরণটিতে - চিহ্ন গুন করা হল)
x=y-7 --------4.Noসমীকরণ তৈরি করা হল

এখন 3.Noসমীকরণ ও 4.Noসমীকরণ দুটির ডানপক্ষে x থাকার কারনে সমীকরণ দুটির ডানপক্ষ সমান | অতএব 3.No সমীকরণ ও 4.No সমীকরণ দুটির বামপক্ষে সমান হবে | অর্থাৎ 117-y =y-7 | এখান থেকে y এর মান পাওয়া যাবে | y এর মান 1.No সমীকরণ অথবা 2.No সমীকরণে বসালে x এর মান পাওয়া যাবে |

117-y =y-7
-y-y=-7-117
-2y=-124
2y=124
y=62

y এর মান 1.No সমীকরণে বসিয়ে পাই
x+y=117--------1.Noসমীকরণ
x+62=117 (y এর মান বসিয়ে)
x=117-62
x=55

x=55, y=62

পদ্ধতি	সমাধান পদ্ধতি
সমীকরণ-i থেকে x- কে y-এর আকারে প্রকাশ করতে হবে \| অনুরূপভাবে সমীকরণ-ii থেকে x- কে y-এর আকারে প্রকাশ করতে হবে \|	সমীকরণ-i থেকে পাই x+y=117 x=117-y সমীকরণ-ii থেকে পাই y-x=7 -x=7-y x=y-7
নির্ণয় করা সমীকরণ দুটির মান সমান ধরে y- সম্বলিত সমীকরণ লিখিব \|	117-y=y-7
y- সম্বলিত সমীকরণ সমাধান করব	117-y=y-7 -y-y=-7-117 -2y=-124 2y=124 y=62
y-এর মান যে কোনো একটি সমীকরণে বসিয়ে x-এর মান নির্ণয় করব	আমি এখানে 1.NO সমীকরণে y-এর মন বসালাম x+y=117 x+62=117 x=117-62 x=55
তা হলে x ও y এর মান হলো, x=55, y=62

পরিবর্ত পদ্ধতি(Method of Substitution)

পরিবর্ত পদ্ধতি এর নিয়ম হল | 1.NO সমীকরণে y এর মান নির্ণয় করতে হবে | 1.NO সমীকরণ থেকে y এর মান নির্ণয় করার পর 2.NO সমীকরণ এর মধ্যে y এর জায়গায় 1.NO সমীকরণ থেকে নির্ণয় করা y এর মান বসাতে হবে | অর্থাৎ মান বসানোর পর 2.NO সমীকরণে চলরাশি y থাকবে না, শুধুমাত্র চলরাশি x থাকবে | এর পর সমাধান করলে x এর মান পাবো | আর x এর মান 1.NO অথবা 2.NO সমীকরণে বসালে y এর মান পাবো |

একটি উদাহরণ এর মাধ্যমে দেখে নেওয়া যাক
x+y=117--------1.Noসমীকরণ
y-x=7--------2.Noসমীকরণ

প্রথমে x+y=117--------1.No সমীকরণ থেকে y এর মান নির্নয় করব |

x+y=117
y=117-x (এটি হল y এর মান )

y এর মান x-y=7 সমীকরণে অর্থাৎ 2.No সমীকরণে বসালে সমীকরণ টি হবে নিম্নরূপ

OR= x-(117-x)=7 (y এর মান বসিয়ে পাই)
OR= x-117+x=7
OR= 2x=7+117
OR= 2x=124
OR= x=62
অতএব x এর মান হল 62

আমি 1.NO সমীকরণে x এর মান বসিয়ে পাই, অর্থাৎ 1.NO সমীকরণে x এর পরিবর্তে 62 বসালে y এর মান পাবো |

x+y=117--------1.Noসমীকরণ
OR 62+y=117 (x এর মান বসিয়ে পাই)
OR y=117-62
OR y=55

পদ্ধতি	সমাধান পদ্ধতি
যেকোনো একটি সমীকরণ থেকে x-কে y-এর আকারে প্রকাশ করতে হবে \| আমি সমীকরণ-i থেকে x-কে y-এর আকারে প্রকাশ করিলাম \| অর্থাৎ x-এর মান নির্ণয় করিলাম \|	সমীকরণ-i থেকে পাই x+y=117 x=117-y
নির্ণয় করা x-এর মান অপর সমীকরনে বসাতে হবে \|	y-x=7 x-এর মান বসিয়ে পাই y-(117-y)=7 y-117+y=7 2y=7+117 2y=124 y=62
এর পর y-এর মান যে কোনো সমীকরণে বসালে x-এর মান পাওয়া যাবে \|	আমি এখানে 2.NO সমীকরণে y-এর মন বসালাম y-x=7 62-x=7 -x=7-62 -x=-55 x=55
তা হলে x ও y এর মান হলো, x=55, y=62

অপনয়ন পদ্ধতি(Method of Elimination)

অপনয়ন পদ্ধতিতে অঙ্ক করার সময় সমীকরণ দুটির x এর সহগ সমান করা হয় | তারপর প্রথম সমীকরণ থেকে দ্বিতীয় সমীকরণ বিয়োগ করে x-এর সহগ সহ x বাদ দেওয়া হয় | তার পর y এর মান পাবো | এরপর পাওয়া y এর মান 1.No অথবা 2.No সমীকরণের যেকোনো একটিতে বসিয়ে সমাধান করলে x এর মান পাওয়া যাবে |

একটি উদাহরণ এর মাধ্যমে বুঝে নেওয়া যাক | বাপন ও উত্তম এর অঙ্কে থেকে পাওয়া সহ সমীকরণ এর সমাধান করার চেষ্টা করি |
x+y=117--------1.Noসমীকরণ | (কারণ দুজনের মোট নাম্বার)
y-x=7--------2.Noসমীকরণ |(দুই বন্ধুর নম্বরের পার্থক্য 7)
y+x=117--------1.Noসমীকরণ টি এই রকম ভাবে লিখতে পারি
y-x=7--------2.Noসমীকরণ

1.Noসমীকরণ ও 2.Noসমীকরণ এ x এর সহগ 1 | অর্থাৎ দুটি সমীকরণ এ x এর সহগ সমান আছে | তাই সমীকরণ দুটির x এর সহগ সমান করার জন্য কোনো সংখ্যা গুন করা হলো না | আর সহগ সমেত চলরাষির চিহ্নের পরিবর্তন করা হল না | কারণ 1.NO সমীকরণের সহগ সমেত চলরাশির চিহ্নের (+) আছে অর্থাৎ (+x) আছে | আর 2.NO সমীকরণের সহগ সমেত চলরাশির চিহ্নের (-) আছে অর্থাৎ (-x) আছে | তাই 1.NO সমীকরণ থেকে 2.NO সমীকরণের সহগ সমেত xচলরাশি বিয়োগ হয়ে যাবে |

y+x=117--------1.Noসমীকরণ
y-x=7--------2.Noসমীকরণ
y+y=117+7--------3.Noসমীকরণ
2y=124
y=62

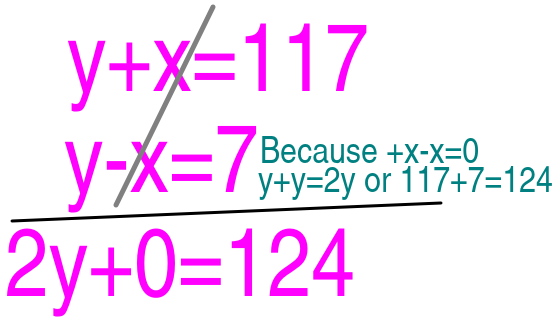
এর পর y-এর মান যে কোনো সমীকরণে বসালে x-এর মান পাওয়া যাবে |

অন্য উদাহরণ এর মাধ্যমে বুঝে নেওয়া যাক |
5y-3x=9--------1.Noসমীকরণ
2y+5x=16--------2.Noসমীকরণ

এখানে দুটি সমীকরণে x এর সহগ গুলি আলাদা | যেমন 1.Noসমীকরণে x এর সহগ হল 3 ও 2.Noসমীকরণে x এর সহগ হল 5 | তাই এখানে 1.No সমীকরণে ও 2.No সমীকরণে x এর সহগ সমান করতে হবে | তাই 1.No সমীকরণ এর সঙ্গে 5 গুন করব, সমীকরণে 5 গুণ করার পর সমীকরণটি হবে (5y-3x=9)\(\times\)5 অর্থাৎ 25y-15x=45 হবে | 25y-15x=45 এই নতুন সমীকরণটির নাম দেবো 3.No সমীকরণ |2.No সমীকরণ এর সঙ্গে 3 গুন করব, সমীকরণে 3 গুণ করার পর সমীকরণটি হবে (2y+5x=16)\(\times\)3 অর্থাৎ 6y+15x=48 হবে | 6y+15x=48 এই নতুন সমীকরণটির নাম দেবো 4.No সমীকরণ |

25y-15x=45--------3.Noসমীকরণ
6y+15x=48--------4.Noসমীকরণ

নতুন পাওয়া 3.NO ও 4.NO সমীকরণে x এর সহগ সমান হয়েছে | তাই 3.NO ও 4.NO সমীকরণ থেকে x এর সহগ সমেত x কে বাদ দিতে পারবো | x চলরাশি সমেত x এর সহগ বাদ দিলে বাকি থাকবে y সমেত y এর সহগ | অর্থাৎ 15x-15x=0 হবে , আর 25y+6y যোগ হয়ে 31y হবে | অতএব 3.NO ও 4.NO সমীকরণ যোগ/ বিয়োগ করার পর নতুন যে 5.NO সমীকরণ পাবো তা হবে 31y+0=93 | 31y+0=93 এটি হলো 5.NO সমীকরণ | এই সমীকরণ সমাধান করলে y এর মান পাবো | y এর মান 1.NO অথবা 2.NO সমীকরণে বসালে x এর মান পাবো |

অন্য উদাহরণ এর মাধ্যমে বুঝে নেওয়া যাক |
2x+3y=7--------1.Noসমীকরণ
3x+2y=8--------2.Noসমীকরণ

এখানে দুটি সমীকরণে x এর সহগ গুলি আলাদা ও চিহ্ন গুলি একই ধরনের | যেমন 1.Noসমীকরণে x এর সহগ হল 2 ও চিহ্ন (+), 2.Noসমীকরণে x এর সহগ হল 3 ও চিহ্ন (+) | তাই x এর সহগ সমান করতে হবে |

2x+3y=7--------1.Noসমীকরণ \(\times\)3
3x+2y=8--------2.Noসমীকরণ \(\times\)2

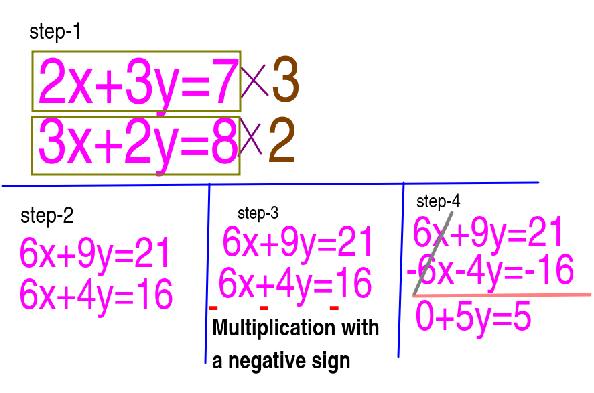
6x+9y=21--------3.Noসমীকরণ
6x+4y=16--------4.Noসমীকরণ

যেহেতু 3.Noসমীকরণ ও 4.Noসমীকরণ এ সহগ সমেত x চিহ্ন + | অর্থাৎ দুটি সমীকরণ এ +6x আছে | তাই 4.Noসমীকরণ এর সাথে বিয়োগ চিহ্ন গুণ করব 6x+4y=16--------4.Noসমীকরণ\(\times\)(-) | বিয়োগ চিহ্ন গুণ করার পর সমীকরণটি হবে (-6x-4y=-16) | এখন 3.Noসমীকরণ থেকে 4.Noসমীকরণ বিয়োগ করা যাবে | অর্থাৎ সহগ সমেত x কে বাদ দেওয়া যাবে |

এর পর y-এর মান যে কোনো সমীকরণে বসালে x-এর মান পাওয়া যাবে |

সহ সমীকরণ এর অঙ্ক গুলি অপনয়ন পদ্ধতিতে এই রকম ভাবে সমাধান করতে হয় |

1.NO ও 2.NO সমীকরণ এ আলাদা আলাদা সংখ্যা গুন করার পর x- যুক্ত পদ দুটি একই হবে
সংখ্যা গুন করার পর পাওয়া পরিবর্তিত সমীকরণ দুটি থেকে x-যুক্ত পদকে অপনীত করতে হবে | অর্থাৎ x-যুক্ত পদকে বাদ দিতে হবে
যদি দুটি সমীকরণে x-যুক্ত পদ এর চিহ্ন সমান হয় তাহলে একটি সমীকরণ কে বীপরিত চিহ্ন দিয়ে গুন করতে হবে | অর্থাৎ দুটি সমীকরণে x-যুক্ত পদ এর চিহ্ন যোগ (+) থাকলে একটি সমীকরণ কে বীপরিত চিহ্ন বিয়োগ (-) দিয়ে গুন করতে হবে |
এর পর y এর মান পাবো
y এর মান পাওয়ার পর 1.NO অথবা 2.NO সমীকরণে y এর মান বসালে x এর মান পাবো

বজ্রগুণন পদ্ধতি(Method of Cross-multiplication)

বজ্রগুণন পদ্ধতি এর সাহায্যে একঘাত সহ-সমীকরণ এর অঙ্ক গুলি খুব সহজেই সমাধান করা যায় | এখানে আমরা x ও y এর মান এক সঙ্গেই নির্ণয় করতে পারবো | বজ্রগুণন পদ্ধতিতে একঘাত সহ-সমীকরণ এর অঙ্ক গুলি কিভাবে সমাধান করব তা দেখে নেওয়া যাক |

4x+3y=17=0--------1.Noসমীকরণ
6x+5y=27=0--------2.Noসমীকরণ
বজ্রগুণন পদ্ধতিতে এই অংকটা কিভাবে করব তার সূত্র |

প্রথমে 1.NO ও 2.NO সমীকরণ এর ডানপক্ষের অঙ্কগুলি বাম পক্ষে নিয়ে আসব | তারপর 1.NO ও 2.NO সমীকরণ এর বামপক্ষে শূন্য থাকবে | অর্থাৎ সমীকরণ দুটি হবে নিম্নরূপ |
4x+3y-17=0--------1.Noসমীকরণ
6x+5y-27=0--------2.Noসমীকরণ

এখানে 1.No সমীকরণ এর অঙ্ক গুলিতে x এর সহগ 4 ও y এর সহগ 3 আছে ও ধ্রুবক পদ হল 17| আর 2.No সমীকরণ এর অঙ্ক গুলিতে x এর সহগ 6 ও y এর সহগ 5 আছে ও ধ্রুবক পদ হল 27| এখন ছবির মতো করে x ও y এর সহগ ও ধ্রুবক পদ গুলি লিখিব |

অর্থাৎ সূত্রটি হল নিম্নরূপ |
\(a_{1}x+b_{1}y-17=0\)--------1.Noসমীকরণ
\(a_{2}x+b_{2}y-27=0\)--------2.Noসমীকরণ
এখানে\( a_{1},a_{2},b_{1},b_{2}\) হল বাস্তব সংখ্যা

দ্বিঘাত সমীকরণ (Quadratic equation)

যে সমস্ত সমীকরণের চলরাশির অর্থাৎ অজানা রাশির সর্বোচ্চ ঘাত(power) দুই হয় সেই সমস্ত সমীকরণ কে বলা হয় দ্বিঘাত সমীকরণ |

একটি দ্বিঘাত সমীকরণ \(ax^{2}+bx+c=0\) এই রকম হয়ে থাকে | যেখানে a,b,c তিনটি হল ধ্রুবক অর্থাৎ বাস্তব সংখ্যা | এখানে a এর মান 0 হবে না , অর্থাৎ \(a\neq 0\) | একটি দ্বিঘাত সমীকরণের দুটির বেশি বীজ থাকবে না |

\(x^{2}+5x-204=0\) এই সমীকরণটির বাস্তব সংখ্যার মান গুলো হল যথাক্রমে a=1,b=5,c=-204
\(x^{2}-x=0\) এই সমীকরণটির বাস্তব সংখ্যার মান গুলো হল যথাক্রমে a=1,b=-1,c=0
\(x^{2}-36=0\) এই সমীকরণটির বাস্তব সংখ্যার মান গুলো হল যথাক্রমে a=1,b=0,c=-36 || 0 এর সঙ্গে x গুন করলে উত্তর 0 হবে তাই এখানে সমীকরণটি হবে \(x^{2}+0\times x-36=0\)
\(3x^{2}+16x-3584=0\) এই সমীকরণটির বাস্তব সংখ্যার মান গুলো হল যথাক্রমে a=3,b=16,c=-3584

দ্বিঘাত সমীকরণ এর প্রকারভেদ

দ্বিঘাত সমীকরণ কে দুই ভাগে ভাগ করা যায় | অমিশ্র বা শুদ্ধ (pure), এবং মিশ্র (adfected)

অমিশ্র বা শুদ্ধ দ্বিঘাত সমীকরণ

যে সমস্ত দ্বিঘাত সমীকরণের চলরাশির দুই ঘাত যুক্ত পদ থাকে কিন্তু এক ঘাত যুক্ত পদ থাকে না সেই সমস্ত সমীকরণকে বলা হয় অমিশ্র বা শুদ্ধ দ্বিঘাত সমীকরণ |

উদাহরণ

\(x^{2}-4=0\) এখানে চলরাশির এক ঘাত যুক্ত পদ অনুপস্থিত অর্থাৎ সমীকরণে চলরাশির এক ঘাত যুক্ত পদ নেই |
\(25x^{2}-100=0\)
\(4x^{2}+5=105\)
ETC

মিশ্র দ্বিঘাত সমীকরণ

যে সমস্ত দ্বিঘাত সমীকরণের চলরাশির দুই ও এক ঘাত যুক্ত পদ থাকে সেই সমস্ত সমীকরণকে বলা হয় মিশ্র দ্বিঘাত সমীকরণ |

উদাহরণ

\(x^{2}+2x-10=0\)
\(3x^{2}+16x-3584=0\)
ETC